・数学 ・応用 ・三平方の定理 ★リクエスト募集中!!( ˙罒˙ ) 学年 中学3年生, 教科書 新版 数学の世界3 大日本, 単元 三平方の定理,三平方の定理と図形の計量,三平方の定理の利用, キーワード 三平方の定理,流花note有料講座 応用問題 三平方の定理(ピタゴラスの定理)について、 定理の証明から、 計算練習までを勉強します。 無料講座の解説資料 中3数学講座第7章(1)三平方の定理 基本pdf 有料講座をご覧いただくにはログインが必要です。三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題と

2重根号の外し方 おいしい数学
三平方の定理 問題 応用
三平方の定理 問題 応用-三平方の定理の空間図形への応用の問題。数学の基礎問題を中心に掲載。普段の家庭学習や定期テスト・受験勉強に! 中学生 勉強なんて 怖くない ~ 勉強が苦手な中学生のために ~ TOP > 中学3年 数学 練習問題一覧 > 三平方の定理/空間図形への利用(1) 勉強しないで後悔するくらい各単元の「問題一括」または「解答一括」をクリックすると、新しいウィンドウ(またはタブ)にPDFファイル が表示されます。保存または直接印刷してください。 最初のページに戻る 単 元 名 ページタイトル 単元別一括 1 式の計算 多項式と単項式の乗除(1) 問題一括 (10,051Kb) 解答一括 (11




三平方の定理 特別な直角三角形 イ弋マ本ゼミナール
三平方の定理の応用 → 携帯版は別頁 三平方の定理 問題1 右図において x , y の長さを求めなさい. x= y= 採点する やり直す 解説 2 x 2 =(4) 2 7x 2 =32 x 2 =25 x=5 (>0) 2 5 2 =y 2 y 2 =36 y=6 (>0) 問題2 右図において CD の長さ x を求めなさい. x= 採点する やり直す 解説 直角三角形 ABC について三平三平方の定理の一般角への応用 三平穂の定理は、あくまでも直角三角形において成り立つ定理ですが、一般角においてはどうなるのでしょうか。それは、高校数学で学ぶ、第二余弦定理というもので、以下のように表されます。 c² = a² b² – 2ab・cosC三平方の定理 発展問題まとめ お疲れ様でした! 入試などの発展問題では、今回のように 三平方の定理を使って、方程式を作ることで 長さを求めていくようになります。 まずは、求めたい部分を\(x\)とする。 直角三角形の各辺を\(x\)を使って表すことができれば 三平方の定理を使って
今回は『三平方の定理』を『空間図形の問題』に応用して問題を解いてみたいと思います。 目次 問題を解くコツ ①ゴールを見据えて、そのために明らかにすべきところを逆算する。 ②分かるところをひたすら書き出して、攻略の糸口を見つける。 実際イ 三平方の定理の活用 ① 面積 (1年平面図形への応用問題) 面積に応用という訳ではありませんが、 面積を求める時に、「三平方の定理」はよく役立ちますね! ですが、あくまで「面積」の問題であって、「三平方」の問題ではないですね! 《 例 》三平方の定理 三平方の定理 平面図形の応用 無料で使える中学学習プリント http//chugakumanabihirobanet/ 2 解答
Acbで三平方の定理を使うと ac 2 = 4 2 2 2 よってac=2 3 cb=2で半径2cmなのでoc=ob=cb となり obcは正三角形。∠cob=60° よって∠cab=30°、 caeは二等辺三角形 なので∠ace=∠aec=75° oe = ae aoなので 2 3 2 oceで∠oec=75°、∠coe=60°、 ∠oce=45°、eからocに垂線を引いて その交点をpとする。・・・図2 図2 p oepは90 三平方の定理は別名ピタゴラスの定理と言い、それを満たす整数をピタゴラス数と言います。 その三つの数を ( a, b ,c )とします。自然数m , n を用意すると、 ( a, b ,c )は次のようにあらわすことができます。 a=m^2n^2 , b=2mn , c=m^2n^2三平方の定理は,中学校の図形教材の最後にあたり,図形分野のまとめとして扱うことのできる 教 基本の問題 1 時間 4 三平方の定理の利用 4 時間 (本時 第1 時間目) 5 いろいろな問題 2 時間 6 基本の問題 1 時間 7 まとめ 1 時間 2 9 単元の評価規準 関心・意欲・態度 数学的な 見方や考え方
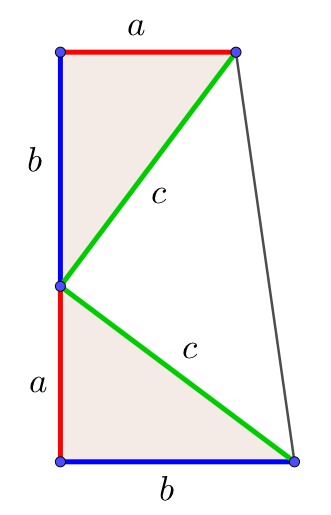



三平方の定理の証明3 大統領の台形 キソカラ




三平方の定理の応用問題 中学3年数学 Youtube
方べきの定理の応用 次は、平成31年度神奈川県高校入試数学の問題です。面白そうな問題だと思うので、皆 さん挑戦してみてください。 三平方の定理を用いた、次のような解答もあるかと思いメールしました。 CQ=x、BQ=y とおく。 ABQについて、 (8-x)^2+y^2=7^2 (1) BQCについて、 三平方の定理とは、直角三角形において3辺の長さの関係を表す公式のことをいいます。 直角と隣り合う2辺の長さをそれぞれ a 、 b 、直角の向かい側にある最も長い辺 (斜辺)の長さが c となる直角三角形があるとします。数学 中学3年生の選択ページに戻る 円と三平方の定理 円と接線の問題で、三平方の定理を用いながら解く問題について学習します。 共通接線;



Homeroom 数学の入試問題を解くとき大切なこと 正しい入り口から入らないと問題は解けない 空間図形 三平方の定理 働きアリ



1
お疲れ様でした!いかがでしたでしょうか?都立高校の実際の入試問題でも「三平方の定理」が大活躍します。 またこの問題のように「 三角形の相似 」 の問題との 融合問題 が多いので、相似についてもしっかりと勉強してください。 三平方の定理で高得点を取る必勝法 ここまで詳しく見て199 4 三平方の定理の応用問題 5 底面の半径が 2 cm,母線の長さが 8 cm の円錐について,次の問いに 答えよ。 ⑴ 側面の展開図のおうぎ形の中心角を求めよ。 ⑵ 右の図のように,円錐の側面上をまわるように,点 A から点 A ま問題の設定 解決の計画 生徒のノート 三平方の定理を利用して,平面や空間のいろいろな長さを求めることができる。 point 3 習ったことを使えば, 説明できる!!



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




三角柱の体積を求める問題です 三平方 ピタゴラスの定理の応用です 解ける方解き方 Clear
1 右の図のような abcがあり,頂点aから辺bcに垂線ahをひいてある。 次の問いに答えなさい。 ① bhの長さを求めなさい。 ② abcの面積を求めなさい。 2 右の図のような直方体で,辺bc上に,ap+pgが最小になるように点 pをとる。次の問いに答えなさい。 つまり、下図のようになるよ! ということは、各頂点から点Pまでの長さが 6 6 だから、三平方の定理を用いると、 x2 = 62 –22 x 2 = 6 2 – 2 2 ∴ x2 = 36− 4 = 32 x 2 = 36 − 4 = 32 ∴ x = 4√2 x = 4 2 (x>0より) これを図にするとこう! 三平方の定理の証明⑪(相似を利用した証明1) 21年1月14日 中3数学 平面図形 中3数学 三平方の定理には数百もの証明方法があります。 今回は相似を利用した基本的な証明方法について紹介します。 目次 1 Ⅰ 三平方の定理とは 2




三平方の定理の応用問題が分かりません この問題を教えてください 数学 教えて Goo




知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より
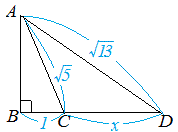
三平方の定理の応用問題 ここまでで、三平方の定理の基礎はだいぶ仕上がってきたと思います。 最後に、少しだけ難易度が上がった応用問題を \(2\) 問解いてみましょう。 応用問題①「1 辺と 1 角から辺の長さを求める」 応用問題① 下の図のような三角形がある。\(a\) の値を求めよ。 角度三平方の定理に関する問題を解くために、定理そのものの他に抑えておくべき重要なポイントがいくつかあります。 おさらいとして三平方の定理は以下の通り。 これに対して、逆も成り立ちます。 三角形の各辺に関して、\(c^2=a^2b^2\)という関係にあるなら、その三角形は直角三角形であるとこの問題も、残りの辺を三平方の定理によって求めることが出来ます! 直角をなす2辺は、定理で示した式の左辺に入るので、\(a=2\)、\(b=3\)として当てはめてみると、 \(2^{2}3^{2}=13=c^{2}\) したがって、 \(c^{2}=49=13\) \(c=\sqrt{13}\) となります。上の直角三角形の分からなかった辺の長さ



三平方の定理の応用




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
図形の応用 円と三平方の定理から最短距離まで 円と三平方の定理;三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題と 三平方の定理の問題がむずしいなぁ〜 と感じたら、以下の点を復習してみてください↓ 三平方の定理の計算のために、復習しておくとよい内容 三平方の定理を使いこなすには、 等式の変形;



かみのドリル 三平方の定理




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学
立体の表面積展開図 (入試問題) (携帯版)メニューに戻る (PC版)メニューに戻る ===三平方の定理の応用=== 三平方の定理 次の図のような直角三角形については b2c2=a2 が成り立つ. 三平方の定理を使えば,直角三角形の2辺の長さが分かれば三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し三平方の定理の逆 z 三平方の定理の応用(平面図形、空間図形など) *「ページ表示」を「見開き」でご覧いただきますと、問題とその 答えが見やすくなります。 *このテキストは家庭学習の補助教材としてのみご利用いただけま す。その他(問題の改変、商用など)の利用はご遠慮




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 2 4
これより三平方の定理を用いて、 A C ² = 4 ² 10 ² A C ² = 4 ² 10 ² A C ² = 116 A C ² = 116 A C = 2 √ 29 A C = 2 29 さらに問題です。 1 1 辺 8cm 8 c m の立方体の頂点や返上の点を結んでできる次の図形(影の部分)の面積を求めなさい。 ただし、点 S S は AE A E の 三平方の定理を使って直角三角形の辺の長さを求める問題です。 心臓を動かす位無意識に使えるようになりましょう。 夢を叶える塾 数学を通して夢を叶える力を育む米沢市の学習塾 フォローする 夢を叶える塾 簡単なご案内;<2節 三平方の定理の応用> 数学への関心・意欲・態度 ・ いろいろな問題の解決に、三平方の定理を利用しようとする。 数学的な見方や考え方 ・ いろいろな図形の中に直角三角形を見いだしたり、補助的につくり出したりするなど、 三平方の定理を適用するための工夫をすることができる




三平方の定理 の問題のわからないを5分で解決 映像授業のtry It トライイット




三平方の定理と円 スタディーx
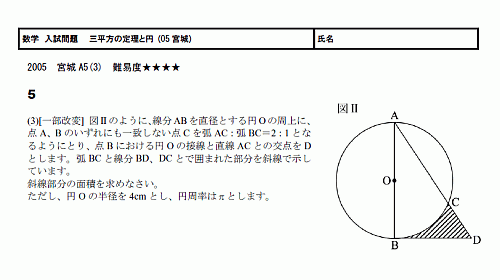
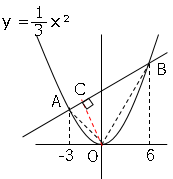
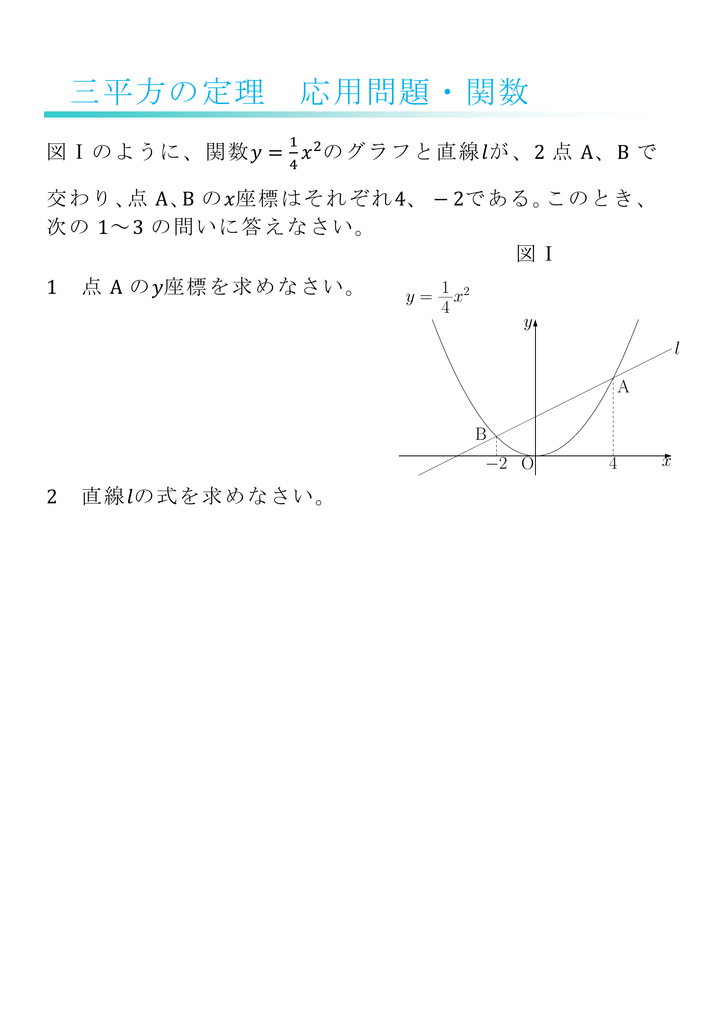
数学37章三平方の定理「三平方の定理の利用」<応用問題> 組 番 名前 1右の図のように,関数 のグラフ 上に点P,χ軸上に点Q(10,0)があります。 POQがOP=OQの二等辺三角形に なるとき,点Pの座標を求めなさい。ただし, 点Pの座標は正の数とします。 2右の図のように,縦,横の長さがそれぞれ5



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース



三平方の定理と円 スタディーx



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス



Studydoctor三平方の定理の利用 中学3年数学 Studydoctor



1




Math 高校入試の難問 三平方の定理 30 60 90 1 2 3と1 2 3 30 60 90 働きアリ



Studydoctor特別な三角形と三平方の定理 中学3年数学 Studydoctor
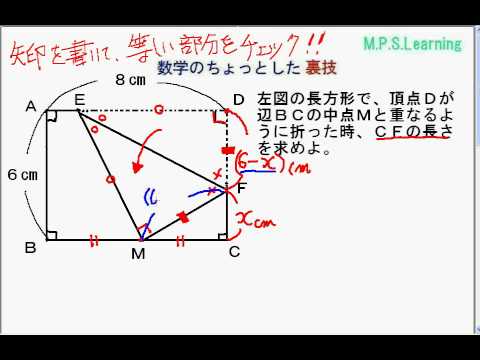



中3数学 三平方の定理の応用 折り曲げ 2 Youtube




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく



三平方の定理 おやじさん ネット



Studydoctor三平方の定理の応用問題 中学3年数学 Studydoctor




中3の数学の問題 セルモ大蔵 世田谷 の塾長ブログ




三平方の定理 ピタゴラスの定理 の証明まとめ5選 全部でいくつあるの 遊ぶ数学



Studydoctor三平方の定理と四角形への利用 中学3年数学 Studydoctor
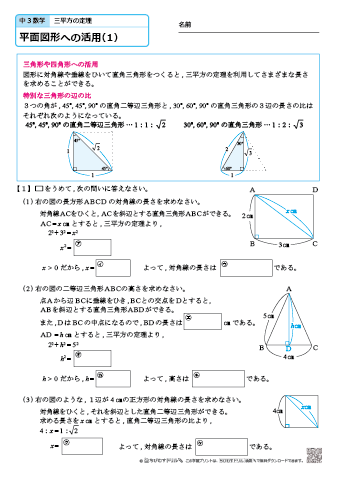



中学3年生 数学 三平方の定理 平面図形への活用 練習問題プリント ちびむすドリル 中学生



中3の数学で三平方の定理の円への応用問題の解き方が分からないので解説して Yahoo 知恵袋




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



数学ia 空間図形の応用問題 広島工業大 東京慈恵会医科大 大学入試数学の考え方と解法




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理 平面図形のいろいろな応用問題 無料で使える中学学習プリント



三平方の定理 練習問題 苦手な数学を簡単に




三平方の定理の練習問題10問 解き方の解説 数学fun




tan8とcos8であらわした三平方の定理の覚え方 Schoolmath S Diary




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく
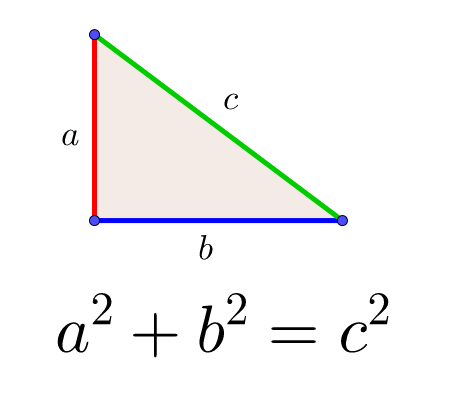



三平方の定理の証明2 4つ直角三角形と真ん中の四角 キソカラ




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学




中3数学 三平方の定理とは 例題編 映像授業のtry It トライイット




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4



中学3年数学練習問題 三平方の定理 空間図形への利用 2




三平方の定理 特別な直角三角形 イ弋マ本ゼミナール




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




三平方の定理の応用




三平方の定理 おやじさん ネット




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース



中3数学応用 おうぎ形と三平方の定理の練習問題 中学生勉強サイトあかね先生




中3数学 三平方の定理の応用 三角形の面積 見方を変える Youtube



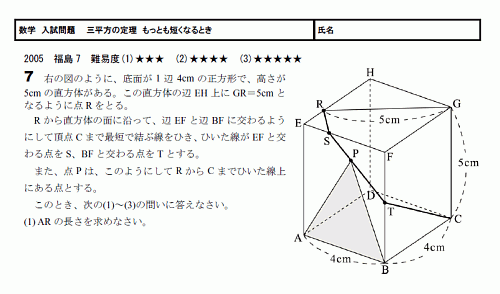
中3数学12 三平方の定理4 空間図形 発展問題プリント 問題 336



三平方の定理 スタディーx




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




無料 中3数学 発展 応用問題 解答プリント 334 三平方の定理2




三平方の定理の応用問題 中学3年数学 Youtube




無料 中3数学 発展 応用問題 解答プリント 336 三平方の定理4 空間図形




無料 中3数学 発展 応用問題 問題プリント 334 三平方の定理2
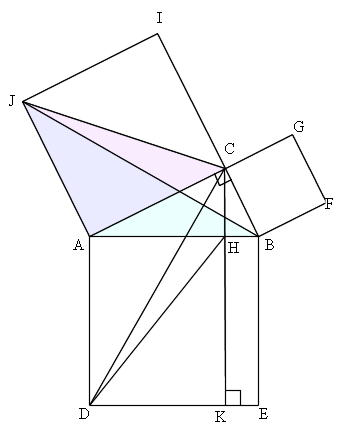



Mathematics 三平方の定理 1 三平方の定理の証明 働きアリ




中3数学 三平方の定理の応用 75度に要注意 Youtube



三平方の定理




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題




三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト



Studydoctor三平方の定理と色々な三角形の面積 中学3年数学 Studydoctor



Studydoctor三平方の定理とよくある辺の比 中学3年数学 Studydoctor




2重根号の外し方 おいしい数学
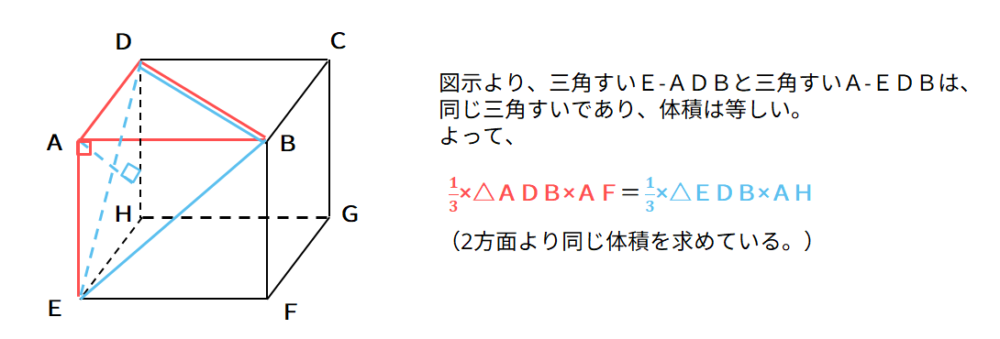



高校入試対策数学 空間図形と三平方の定理の対策問題 中学生勉強サイトあかね先生




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



1




三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori



三平方の定理の応用 3 ネット塾



三平方の定理の練習問題1 数学の要点まとめ 練習問題一覧




Amazon Co Jp 中学 数学 3年 基礎 問題集 6 三平方の定理 Dvd 授業 テキスト 問題集 プロ家庭教師が教える 中学生用学習dvd 中学受験 予習 復習 試験対策 Dvd Rom Pcソフト




ピタゴラスの定理 Wikipedia




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト




三平方の定理 立体 苦手な数学を簡単に




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理 膨大なページ数 Wiki




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集



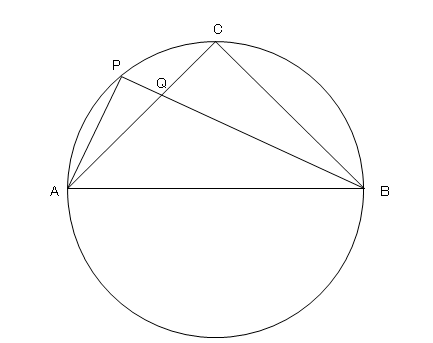
中学数学 三平方の定理 円と接線 弦 中学数学の無料オンライン学習サイトchu Su



三平方の定理 応用問題 関数



Http Www Asahi Okayama C Ed Jp Nyuushi Jouhou H25 Suugaku Kaisetu Pdf
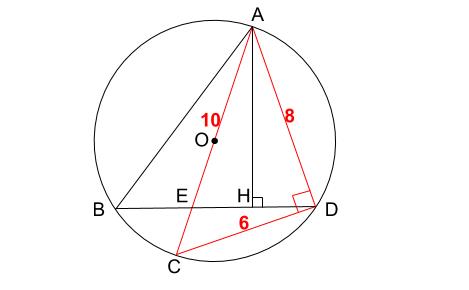



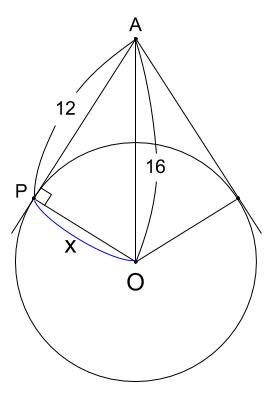
高校入試数学の難問 円 相似と三平方の定理の総合 中学数学の無料オンライン学習サイトchu Su




三平方の定理と相似の問題 無料で使える中学学習プリント
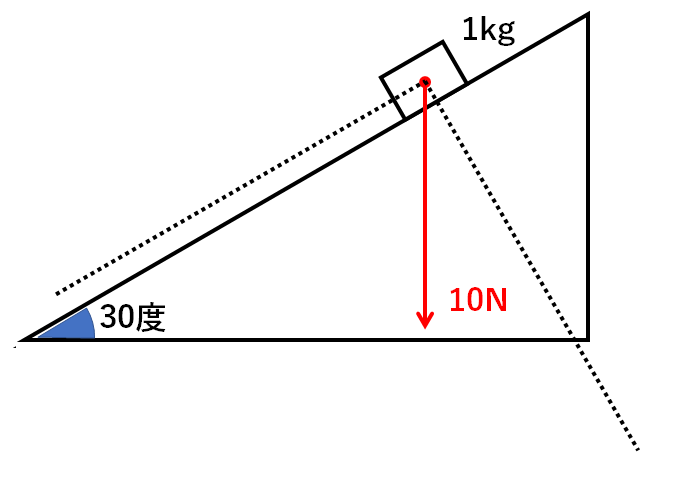



中3物理 分力と三平方の定理 中学理科 ポイントまとめと整理
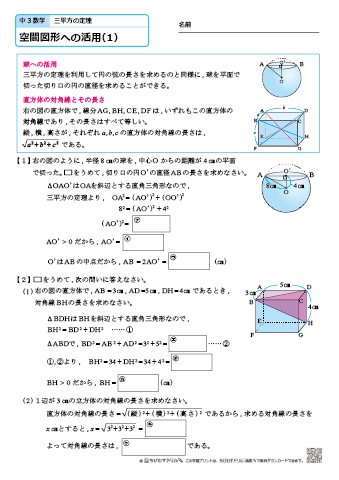



中学3年生 数学 三平方の定理 空間図形への活用 練習問題プリント ちびむすドリル 中学生



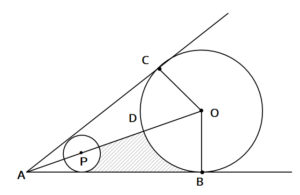
高校入試数学 円と三平方の定理の利用の融合問題



1




三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に



中学三平方の定理の応用の問題です Ad の台形の面積の求 Yahoo 知恵袋




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




無料 中3数学 発展 応用問題 問題プリント 333 三平方の定理1




三平方の定理を利用して四角すい 円すいの体積を求める 無料で使える中学学習プリント
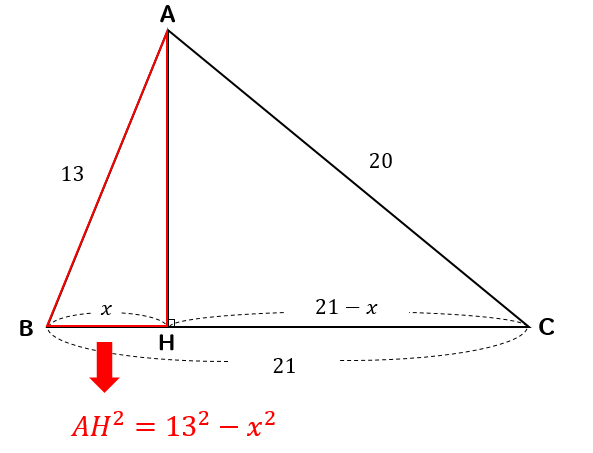



三平方の定理 方程式を利用する発展問題を解説 数スタ
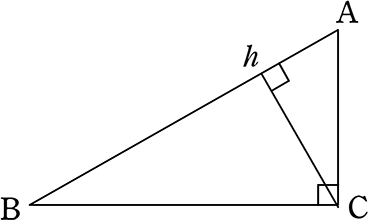



中学数学 三平方の定理
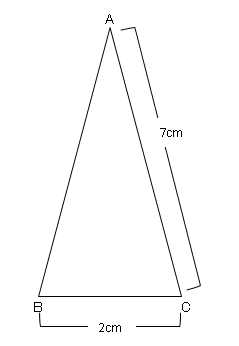



三平方の定理の応用 2 ネット塾
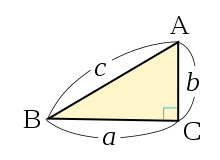



中学校数学 3年生 図形 三平方の定理 Wikibooks




数学 中3 61 三平方の定理 基本編 Youtube




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集



0 件のコメント:
コメントを投稿