[最も人気のある！] 3角形公式 132503

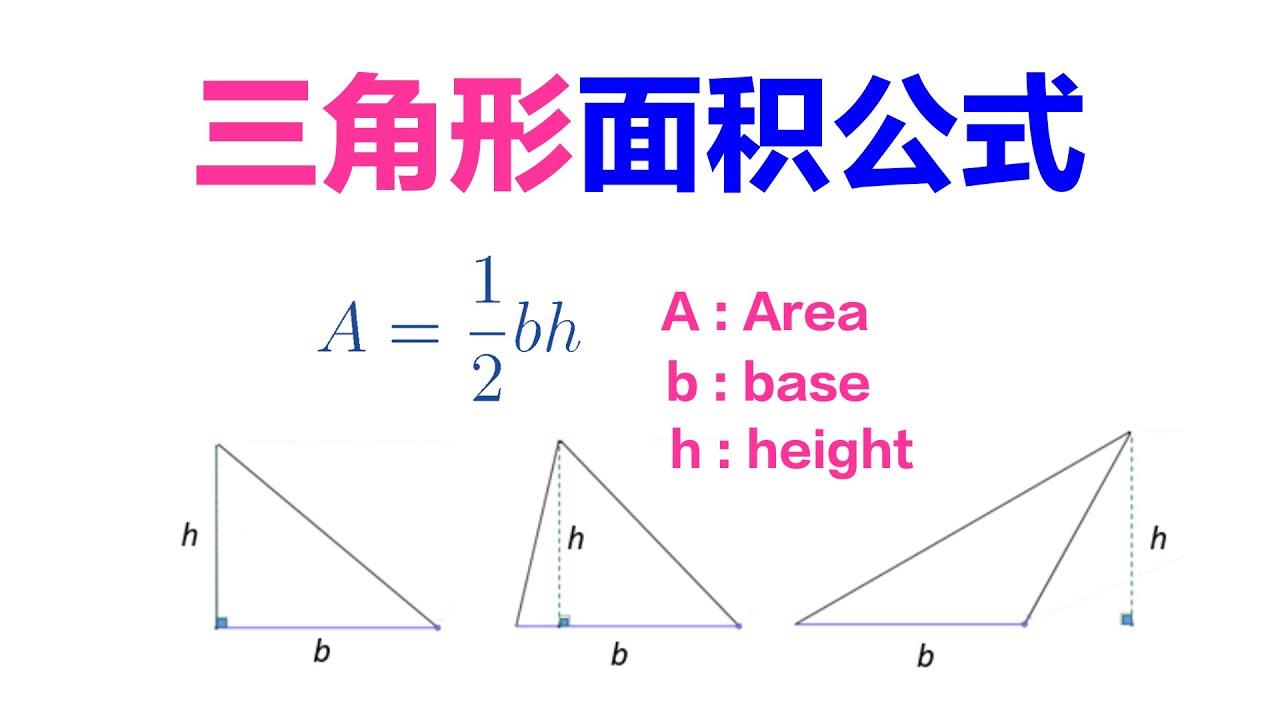
角度が特徴的であるために有名な三角形もあります。 三つの角が ( 3 0 ∘, 6 0 ∘, 9 0 ∘) (30^ {\circ},60^ {\circ},90^ {\circ}) (30∘,60∘,90∘) である直角三角形。 三辺の比が ( 短辺, 斜辺, 長辺) = (\text {短辺},\text {斜辺},\text {長辺})= (短辺,斜辺,長辺) = ( 1 2 3) (12\sqrt {3}) (1 2 3球面三角法（きゅうめんさんかくほう、英 spherical trigonometry ）とは、いくつかの大円で囲まれた球面上の図形（球面多角形、とくに球面三角形）の辺や角の三角関数間の関係を扱う球面幾何学の一分野である。 球面上に2点A,Bがあるとき、この2点と球の中心を通る平面で切断したときの断面に 三角形の面積の公式 三角形の面積には、いくつかの求め方があります。 ここでは、代表的な三角形の面積の公式 \(3\) つを紹介します。 公式①底辺 × 高さ ÷ 2 まず \(1\) つ目は、底辺と高さを使った最もオーソドックスな公式です。

90度等边三角形边长公式 在三角形中角c为90度 90度等边三角形求斜边

3角形公式

3角形公式- =（1/4）√ (abc) (abc) (acb) (bca) 3已知三角形两边a,b,这两边夹角C，则S＝1/2 * absinC 4设三角形三边分别为a、b、c，内切圆半径为r 则三角形面积= (abc)r/2 5设三角形三边分别为a、b、c，外接圆半径为R 则三角形面积=abc/4R四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円 1辺フラット 円 2辺フラット 穴がある四角形

三角形面积公式的证明 Youtube

喺三角形 A B C {\displaystyle ABC\,} 中， 三個角嘅正切同三邊有以下關係： tan ⁡ A 2 = 1 b c − a ( b c − a ) ( a c − b ) ( a b − c ) a b c {\displaystyle \tan {\frac {A} {2}}= {\frac {1} {bca}} {\sqrt {\frac {\left (bca\right)\left (acb\right)\left (abc\right)} {abc}}}} 在上诉求等边三角形面积的时候，用到了勾股定理以及三角形的面积公式：三角形的面积=底×高÷2。 运用等边三角形的三线合一，底边上的高垂直平分底边，求出底边上的高，再根据角形的面积=底×高÷2。用边长表示三角形的面积。 扩展资料： 等边三角形的性质： 為此三角形的外接圓半徑，則存有以下關係式： a sin ⁡ A = b sin ⁡ B = c sin ⁡ C = 2 R = a b c sin ⁡ A sin ⁡ B sin ⁡ C {\displaystyle {\frac {a} {\sin A}}= {\frac {b} {\sin B}}= {\frac {c} {\sin C}}=2R= {\frac {abc} {\sin A\sin B\sin C}}} 由勾股定理得 sin 2 ⁡ θ cos 2 ⁡ θ = 1 {\displaystyle \sin ^ {2}\theta \cos ^ {2}\theta =1} 当

 (2) op 是 角的终边，至于是转了几圈，按什么方向旋转的不清楚，也只有这样，才能说明角是任意的 (3)比值只与角的大小有关 4 三角函数在各象限内的符号规律： 第一象限全为正,二正三切四余弦 四． 诱导公式： 1 终边相同的角的同一三角函数值相等 2 六角形まで確かめてみて「あること」に気づかない？？ そう、じつは、 多角形には「角の数 2」個の三角形がひそんでいる んだ。 「五角形」だったら、 「5」から「2」をひいた「3」個の三角形がかくされているというわけさ。 n角形のときは（n2）個の 解三角形公式整理pdf 2页 8人阅读 （精编整理）高考数学总复习 专题4 三角函数、解三角形 第27练 同角三角函数关系式和诱导公式 （文）（含解析）docx 7页 9人阅读 高中解三角形公式大全(整理版)pdf 3页 34人阅读 解三角形公式整理 3页 3人阅读

直角三角形的中線長和內切圓半徑滿足以下的公式 m a 2 m b 2 = 5 m c 2 = 5 4 c 2 {\displaystyle m_{a}^{2}m_{b}^{2}=5m_{c}^{2}={\frac {5}{4}}c^{2}} 因為直角三角形斜邊的中線長是斜邊的一半，會將直角三角形分為二個 等腰三角形 。年6月29日更新，补充了万能公式。 在《任意角三角函数与诱导公式》一文中，我们详细介绍了利用单位圆来求解任意角的三角函数值。 但是很多角并不是那么容易求得的，因为单位圆求解对应角的三角函数值其本质还是要利用三角形的几何关系，一些特殊的角如 等都很容易得到，如果不是特殊你可以使用这个公式：s = (abc)/2 求出。 例如，三角形三边长为 a = 4、b = 3和c = 5，故而s = (435)/2，也就是s = (12)/2。 求出s = 6。 然后使用海伦公式的第二部分。 面积 = sqr (s (sa) (sb) (sc)。 再将面积代入含有高的面积公式：1/2bh （或 1/2ah 、1/2ch）。 计算求出高。 在本例中，就是1/2 (3)h = sqr (6 (64) (63) (65)。 化简得3/2h = sqr (6 (2) (3) (1)，也就是3/2h = sqr (36)。

直角三角形面积公式直角三角形的面积公式是什么 天奇生活

高二高中數學的 高二數學 三角形面積公式3 6 充實版 筆記 Clear

三角形の辺をa、b、c、角をA、B、Cとします。 三辺の長さが分かれば、ヘロンの公式と三角形の面積の公式を用いて高さを求めます。 二辺と挟まれる角が分かる場合は、A = 1/2ab(sin C)の公式を使って高さを求めます。α, β, γ が三角形の3つの角の大きさのとき、即ち α β γ = π を満たす場合、以下の式が成り立つ。 tan ⁡ α tan ⁡ β tan ⁡ γ = tan ⁡ α ⋅ tan ⁡ β ⋅ tan ⁡ γ {\displaystyle \tan \alpha \tan \beta \tan \gamma =\tan \alpha \cdot \tan \beta \cdot \tan \gamma \,}3角函數 條件 直角3角形, 若其相同, 其邊長成比例 定義 如圖1設 , 並 q 為 與 的夾角 , 則 sin q = 對邊 / 斜邊 , cos q = 鄰邊 / 斜邊 , tan q = 對邊 / 鄰邊 , cot q = 鄰邊 / 對邊 , sec q = 斜邊 / 鄰邊 , csc q = 斜邊 / 對邊 , 以邊長來表示如下 , , , , ,

行测平面几何题公式汇总之三角形篇 三角形 行测 公式 新浪新闻

求直角三角形斜边长直角三角形求斜边长计算公式 朵拉利品网

The latest tweets from @sumi3kaku3角の二等分線に関する重要な3つの公式 D D とおく。 DC=e, AD=f DC = e,AD = f とおくとき以下の公式が成立する。 公式1は辺の比の公式で教科書にも載っています。 公式3はスチュワートの定理の特殊な形で，美しいし応用例も多いので導き方も含めて覚えておい则三角形面积 5设三角形三边分别为a、b、c，外接圆半径为R 则三角形面积=abc/4R S=2R²·sinA·sinB·sinC 6行列式形式 为三阶行列式，此三角形 在平面直角坐标系内 ，这里 选取最好按逆时针顺序从右上角开始取，因为这样取得出的结果一般都为正值，如果不按这个规则取，可能会得到负值，但不要紧，只要取绝对值就可以了，不会影响三角形面积的大小。 该公式的证明

直角三角形面积怎么算性质是什么 初三网

小学数学公式之直角三角形面积公式 尚七培训

S formula (1) area S = √s(s−a)(s−b)(s−c) s= (abc) 2 T r i a n g l e b y H e r o n ′ s f o r m u l a ( 1) a r e a S = s ( s − a) ( s − b) ( s − c) s = ( a b c) 2 お客様の声 アンケート投稿 よくある質問 今天小编给大家分享的这份三角形面积计算公式绝对可以颠覆你对三角形面积计算的认识，以后遇到类似的题目只要直接套用公式即可。 我敢肯定至少到目前为止全网络总结最全的一次。 （一定要为收藏备用） 此次分享的资料和和别的资料最大的区别有两点：1这份三角形面积计算公式从小学到大学都可以用；2从平面到立体。 几何是数学不可或缺的一块版图，不管在(3) 3⋅cot°cot40°−cot°−cot40°= 。提示：考慮cot(40°°) Ans：(1) 3 (2)− 3 (3) 3 (練習8) 設A、B、C 為∆ABC 的內角， 請證明：cot A 2cot B 2cot C 2 = cot A 2⋅cot B 2⋅cot C 2。 (乙)和角公式的應用 善用和角公式的精神：

三角形的面積

锐角三角形的计算公式 3角形面积计算公式 尚书坊

三角形の証明・形状問題 → 携帯版は別頁 → 印刷用PDF版は別頁 三角関数の加法定理，倍角公式，3倍角公式，半角公式 三角関数の和や積には多くの公式がありますが，「 加法定理は覚える，他は作る」 というのが，作者おすすめの考え方です 三角比・三角関数の公式一覧。 正弦・余弦・加法定理など このページでは、 三角比・ 三角関数 の公式 をまとめています。 予習・復習に役立てていただければ嬉しいです。A = 3 4 a 2 {\displaystyle A= {\frac {\sqrt {3}} {4}}a^ {2}} 外接圓 的半徑 R = 3 3 a {\displaystyle R= {\frac {\sqrt {3}} {3}}a} 內切圓 的半徑 r = 3 6 a {\displaystyle r= {\frac {\sqrt {3}} {6}}a} 以上公式可由 勾股弦定理 推導而得。 正三角形的垂足和其底邊的中點共點，因此正三角形的高也是其底邊的 中垂線 及 中線 ，高也會將頂點所的在的角平分。

等角三角形 翰林雲端學院

学军小筑 各种图形计算公式 给孩子留着

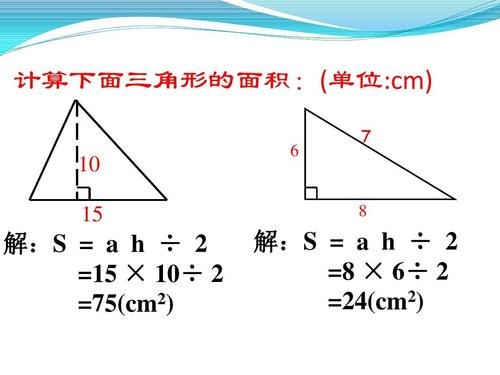
二、从上面的公式，我们知道应该用 正切。 三、计算 对边/邻边 = 300/400 = 075; 三角形ABC = ①×2 = √3/4・a 2 となり、正三角形の面積の公式の証明ができました。 正三角形の面積の公式は知っていると便利ですが、忘れるとかなり危険です。 なぜ正三角形の面積の公式が成り立つのかをしっかり理解しておきましょう！ いかがでしたか？(注意： 12 是 高度，不是左边的边的长度） 高 = h = 12 底 = b = 面积 = ½ × b × h = ½ × × 12 = 1

3种方法来计算三角形的周长

小学三角形的公式 万图壁纸网

Tan x° = 对边/邻边 = 300/400 = 075 tan1 of 075 = 369° （保留一位小数）3倍角の公式とは、角 3α の三角関数（左辺）を、角 α の三角関数に変換する（右辺）公式です。 \begin{align*} \sin3\alpha &= 3\sin\alpha 4\sin^3\alpha \\5pt \cos3\alpha &= 4\cos^3\alpha 3\cos\alpha \\5pt \end{align*} 解斜三角形：（小写字母为边长 大写字母为角度） 在三角形ABC中，角A,B,C的对边分别为a,b,c 则有 1）正弦定理： (R为三角形外接圆半径) 2）余弦定理： 注：勾股定理其实是余弦定理的一种特殊情况。 3）余弦定理变形公式 ：

三角形面积公式 三角形面积万能公式 十安知识网

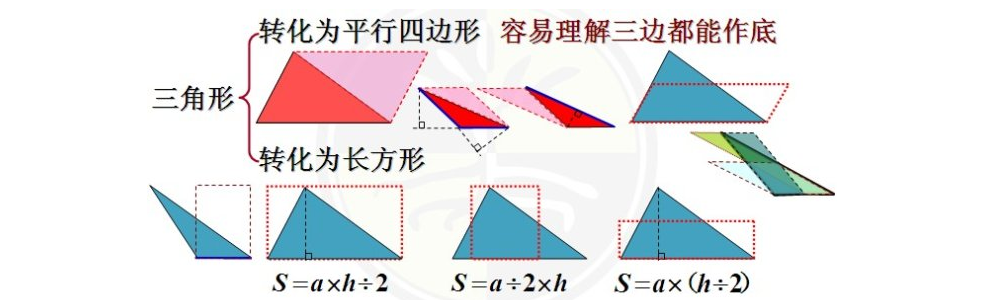
常用的三角形面积公式

如果给出足够的几何属性， 直角三角形计算器 就能自动补全直角三角形的所有属性，如面积，周长，边和角度。 直角三角形是一个具有三个顶点（角）和三个边（边）的多边形，其中两条边以直角相交。 直角三角形 维基百科页面 相关计算器： 三角形计算器 等边三角形计算器 等腰三角形计算器 支持的函数 代入解得s=8√ 3 海伦公式的几种另证及其推广 关于三角形的面积计算公式在解题中主要应用的有： 设 ABC中，a、b、c分别为角A、B、C的对边，ha为a边上的高，R、r分别为 ABC外接圆、内切圆的半径，p = (abc),则 S ABC = aha= ab×sinC = r p公式1：1つが原点である場合 3つの頂点のうち、1つが原点なら、公式はシンプルな形になります。 実際、座標平面上の3点 ( x 1, y 1), ( x 2, y 2), ( 0, 0) を頂点とする三角形の面積は、 1 2 x 1 y 2 − x 2 y 1 となります。 （この公式の証明はページの最後で説明します） 例えば、座標平面上の3点 ( 1, 2), ( 3, 4), ( 0, 0) を頂点とする三角形の面積は、 1 2 1 × 4 − 3 × 2 = 1

等边 正 三角形面积 周长 边长 高在线计算器 三贝计算网 23bei Com

三角形已知边长求高公式 三角形求高为什么面积先要乘以2 图形面积计算公式教学的一些感悟 了不起频道的博客 程序员宅基地

三角形的三条边长分别是 a 、 b 和 c ，周长 P 的公式是： P = a b c 。正多角形の内角と外角の大きさ 具体例で学ぶ数学 > 図形 > 正多角形の内角と外角の大きさ 最終更新日 正多角形の内角の大きさは、頂点の数を n とすれば、 180 ( n − 2) n という公式で計算できます。 正多角形の外角の大きさは、頂点の数を n と

直角三角形面积公式直角三角形的面积公式是什么 天奇生活

直角三角形的斜边计算公式求三角形斜边长公式 朵拉利品网

直角三角形面积公式 100查分网

求三角形面积公式

钝角三角形 面积 周长 边长 高计算公式与在线计算器 三贝计算网 23bei Com

三角形公式 万图壁纸网

等腰三角形面积公式

直角三角形边长公式60度直角三角形公式 尚书坊

四边形的面积公式 三角形的面积公式 尚书坊

45度直角三角形斜边公式30度角所对的直角边是斜边的

90度等边三角形边长公式 在三角形中角c为90度 90度等边三角形求斜边

任意三角形面积公式是什么

1

三角形面积公式 玄数

三角形的面積

三角形的面積

从广勾股定理到斯蒂瓦特定理再到三角形重要线段计算公式 每日头条

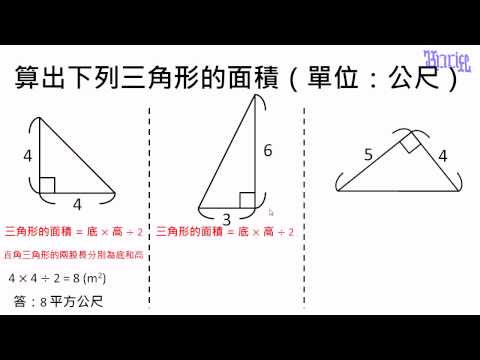
例題 直角三角形面積的計算題1 數學 均一教育平台

坐標里求三角形面積的簡單公式 拓展知識點 中學生可以學學 每日頭條

三角形画像 三角形画像加工アプリ Christinecocajp

三角形面积怎么算公式 好的手游网

三角形 Wikiwand

三角形斜边面积公式直角三角形斜边上的高怎样计算 朵拉利品网

三角形面积公式的证明 Youtube

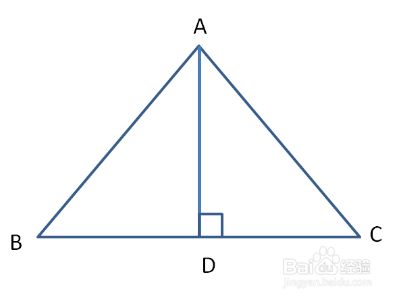
等边直角三角形边长公式和图解 百度经验

11等边三角形面积公式勾股定理初中数学初二 Youtube

1

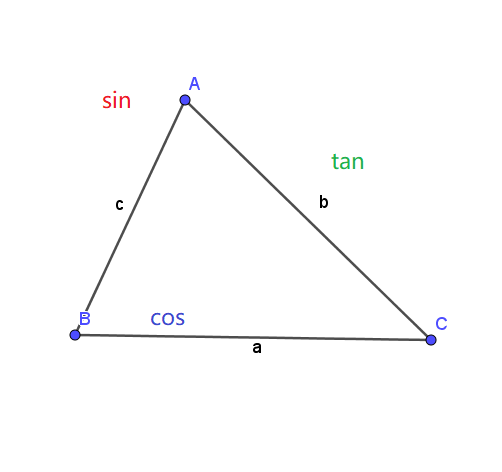
三角形中三角比的特殊公式 知乎

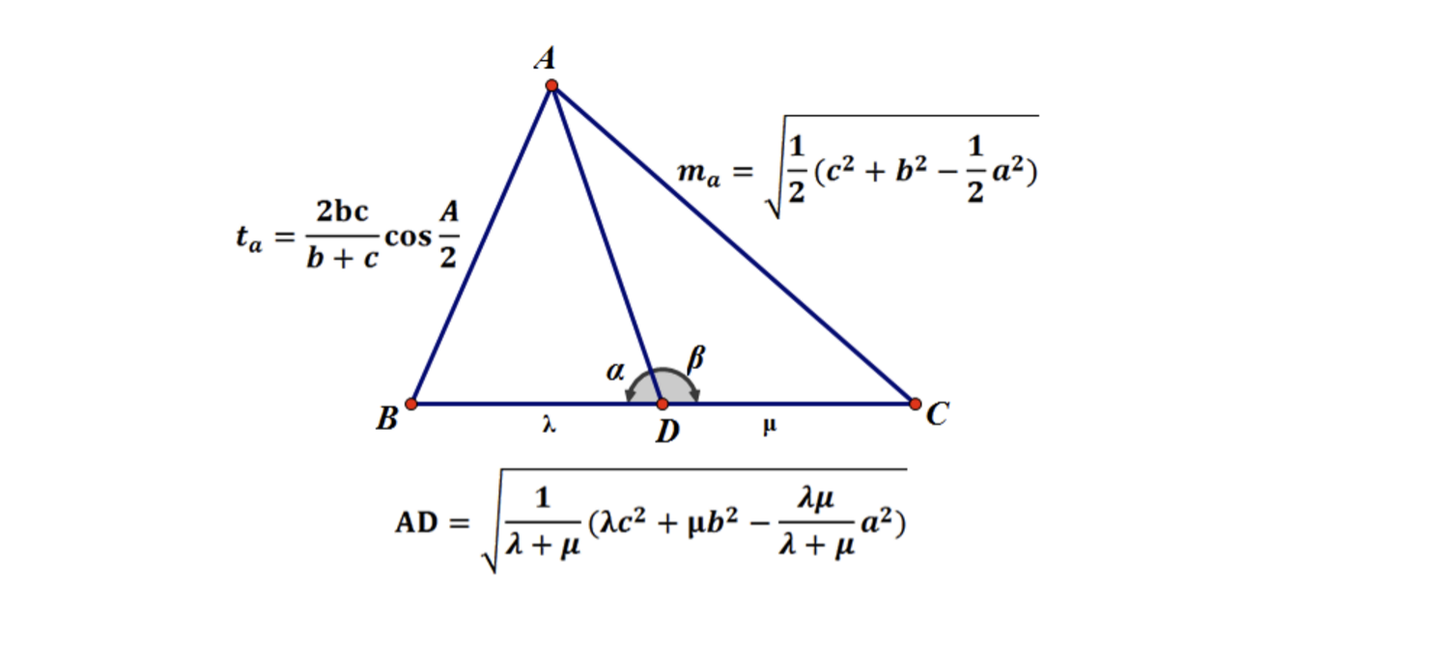
三角形中的线段 知乎

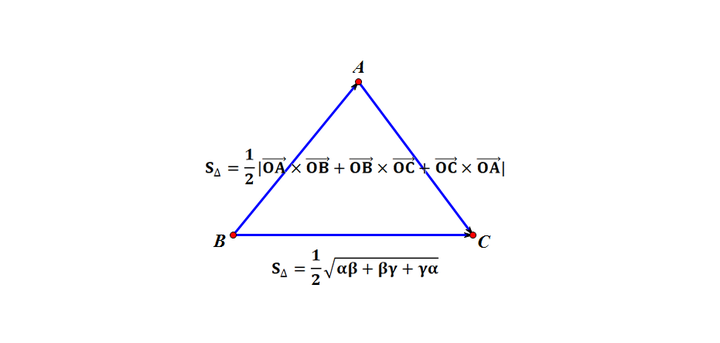
三角形的面积公式九叙 知乎

直角三角形怎么求斜边直角三角形求斜边长计算公式 朵拉利品网

等腰直角三角形面積公式 等腰直角三角形是一種特殊的三角形 具有所有三角形 百科知識中文網

等边三角形边长公式 信息评鉴中心 酷米资讯 Kumizx Com

工作三角形公式幂方程科学公式png图片素材免费下载 图片编号 Png素材网

三角形面积公式x54 小学入门易大学精通难难度三星 哔哩哔哩 つロ干杯 Bilibili

用海伦公式求三角形面积 只知三角形三条边分别是3 5 6 如何求三角形面积 哔哩哔哩 Bilibili

3种方法来计算三角形的周长

锐角三角形 面积 周长 边长 高计算公式与在线计算器 三贝计算网 23bei Com

等边三角形边长公式 信息评鉴中心 酷米资讯 Kumizx Com

等边三角形边长公式 信息评鉴中心 酷米资讯 Kumizx Com

3种方法来计算三角形的周长

三角形 21 直角三角形面積的基本計算題 Youtube

如何计算角度 8 步骤 包含图片

三角形重心的坐标公式推导证明 三角形几何重心的基本性质 哔哩哔哩 Bilibili

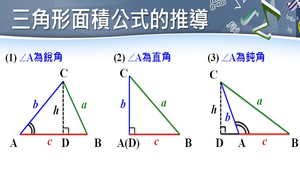
三角形面積公式的推導

三角形的面积公式是怎样推导出来的 用两种方 教育资讯 365bet体育在线投注

已知三角形三点坐标求一边上的高 海伦公式和坐标推导 Chaoyang111的博客 Csdn博客

已知直角三角形的两条直角边求斜边 要公式啊 教育 网赌十大信誉的平台

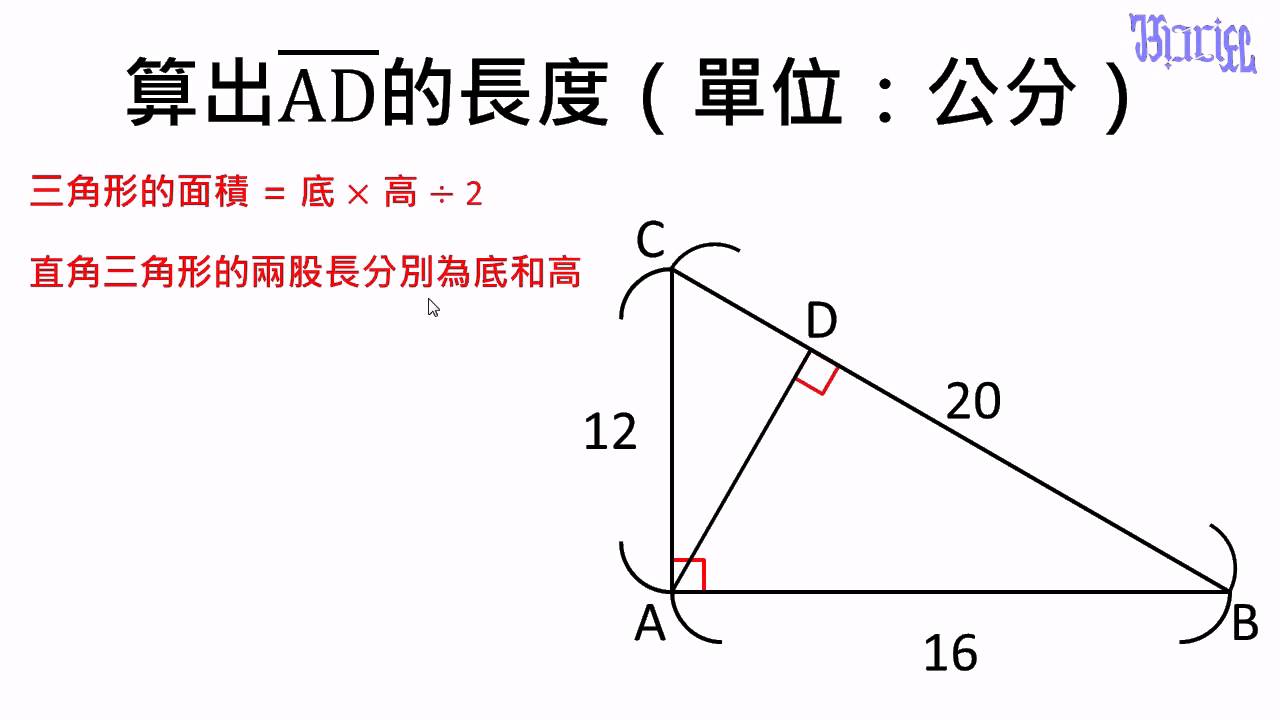
三角形 22 直角三角形面積的進階計算題 Youtube

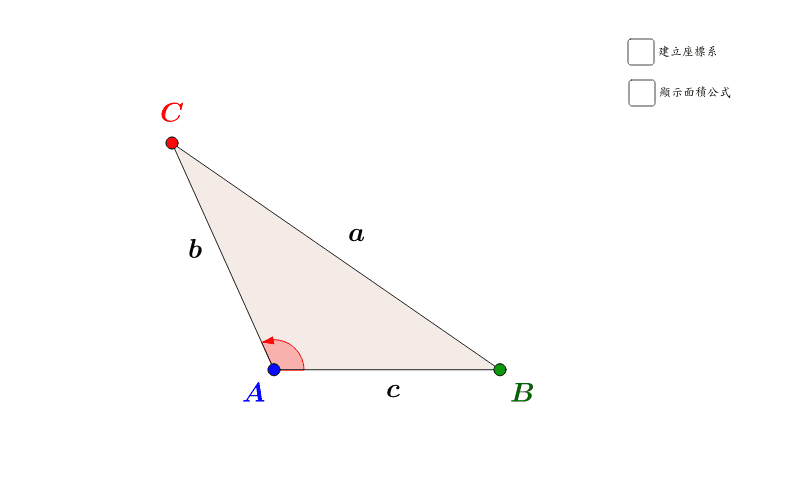
三角形面積公式1 2 Sina Geogebra

一題多解 等腰直角三角形給定斜邊 求面積 Ydm 生活學習誌 痞客邦

Q Tbn And9gcrxib0b6io2em Cewyus2gnkkzp6ipl9bwyzt2fvpkhvnkbj 0c Usqp Cau

三角形的公式 西瓜视频搜索

例題 直角三角形求斜邊或股長 數學 均一教育平台

直角三角形公式面積 直角三角形的面積公式是什么 作業幫 Jvvx

三角形边长公式 搜狗图片搜索

等腰三角形面积 周长 边长 高 顶角 底角在线计算器 三贝计算网 23bei Com

三角形的高公式 直角三角形的高公式 七月seo

十七种三角形面积公式

三角形的面積

海伦公式 已知三边长求三角形面积通解 腾讯视频

直角三角形公式面積 直角三角形的面積公式是什么 作業幫 Jvvx

三角形面积公式 玄数

三角形的高 求三角形高的公式 篆体字转换器

1

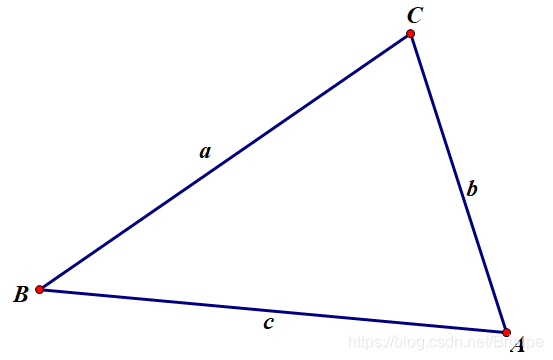
各种三角形边长的计算公式 We Are All In The Gutter But Some Of Us Are Looking At The Stars 程序员宅基地 三角形边长公式

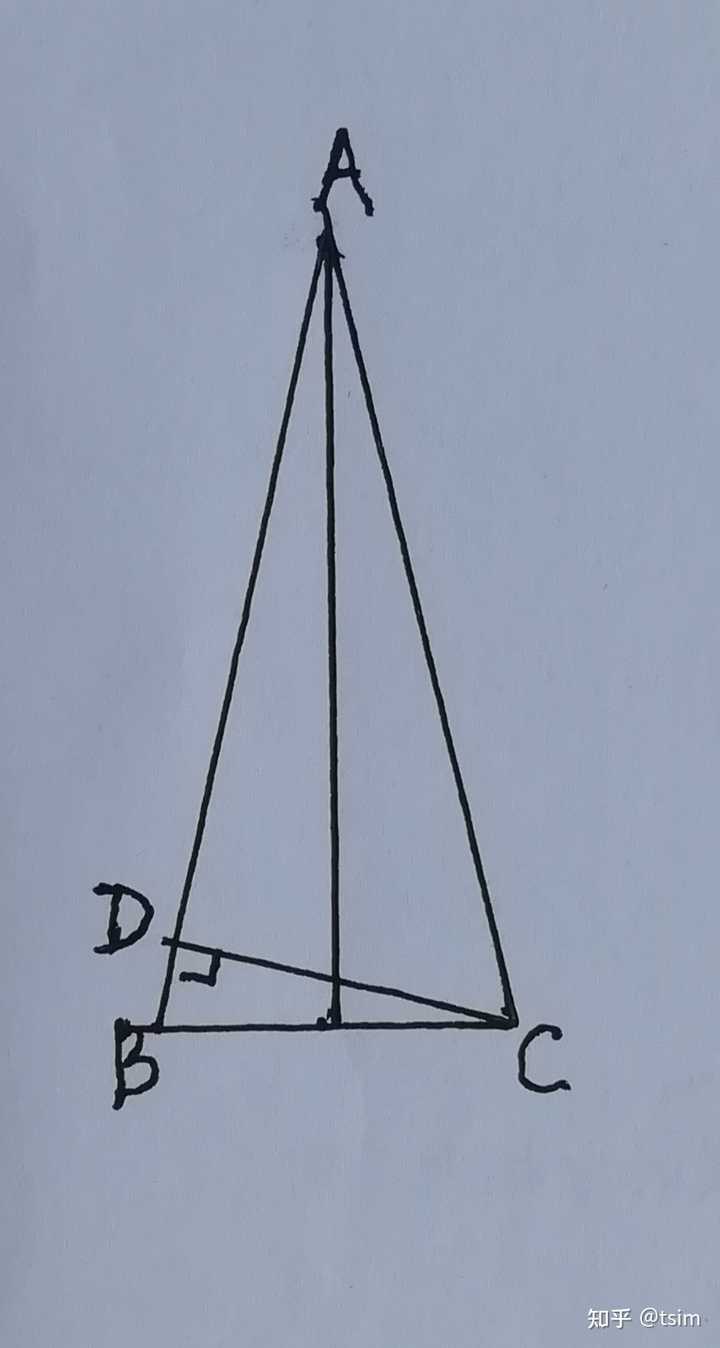
等腰三角形怎么求底边 等腰三角形公式 等腰三角形知道腰求底边

直角三角形公式建筑木工平方计算公式 15直角三角形边长公式

欧拉公式 有关三角形的内外心距离 外接圆

三角形的几个面积公式都是什么时候发现的 网易订阅

三角形面積公式 三角形面積公式是指使用算式計算出三角形的面積 同一平面內 百科知識中文網

正三角形面积公式 搜狗图片搜索

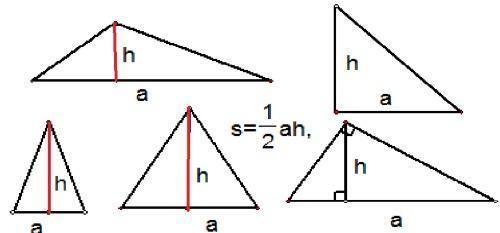
三角形面积公式 搜狗百科

等腰三角形高度公式 角几何png图片素材免费下载 图片编号 Png素材网

数三角形个数公式 万图壁纸网

圆面积公式大全 三角形面积计算公式大全及练习题 尚书坊

三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

三角形边长和面积公式 西瓜视频搜索

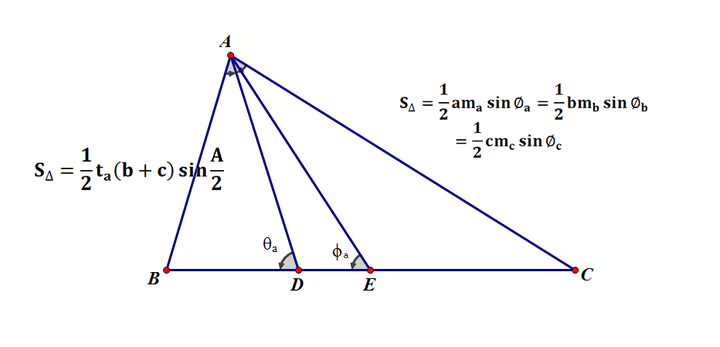
三角形的面积公式七叙 知乎

三角形面积计算公式 三角形面积计算的万能公式 最全知识分享

三角形面积公式 快懂百科

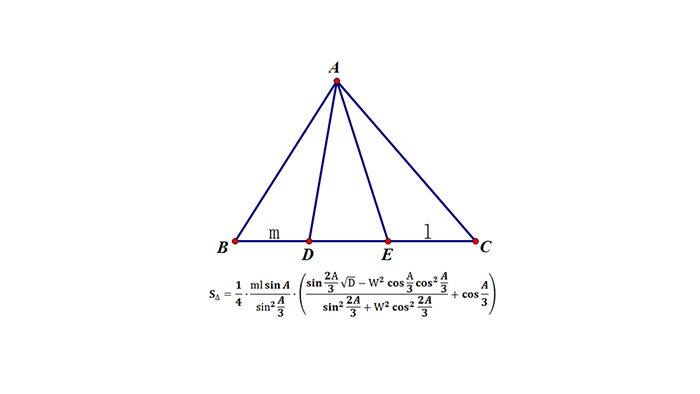
三角形的面积公式十叙 知乎

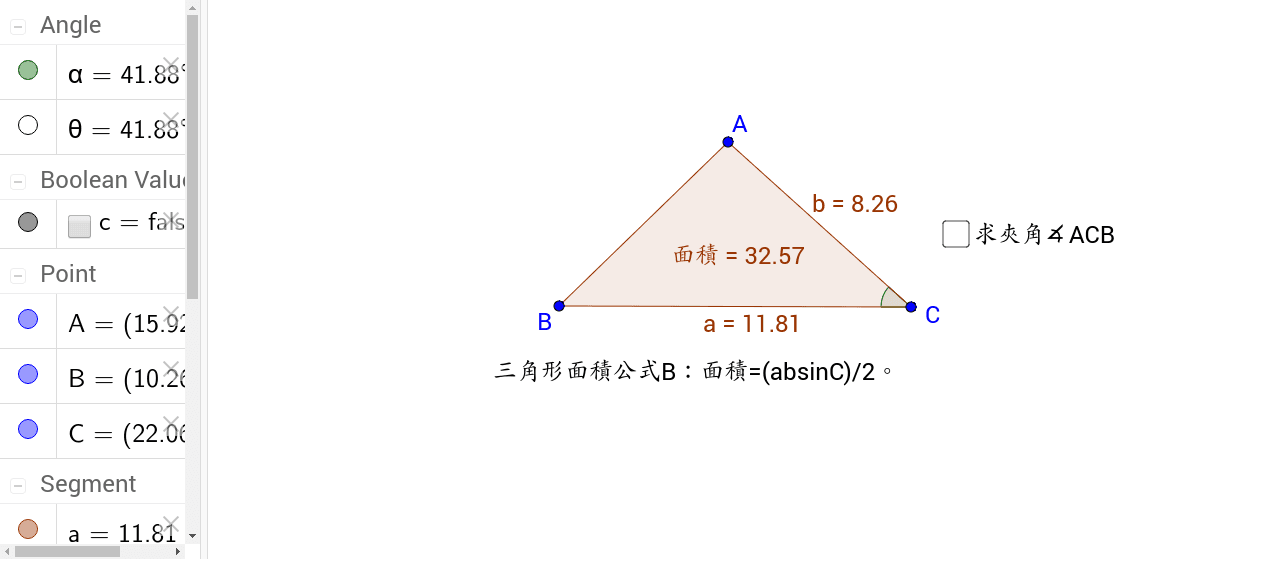
三角形面積公式b2 Geogebra

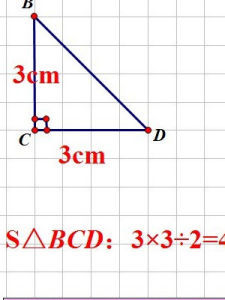
等腰直角三角形面积公式 快资讯

直角三角形 图片欣赏中心 急不急图文 Jpjww Com

直角三角形公式 万图壁纸网

02特殊角的三角函数直角三角形的边角关系初中数学初三 Youtube

三角形面積公式 兩邊一夾角 Youtube